加载应力

在碟型弹簧加载变形过程中，轴向应力很小，可忽略不计，因此其疲劳寿命切向应力影响。通常情况下，碟片上表面承受压应力，下表面承受拉应力。

实际上，碟型弹簧的计算应力与实际应力并不一致，这是由于喷丸处理和强压处理过程中产生的残余应力所致，实际应力由残余应力和加载应力所组成。弹簧的动态强度主要受碟片下表面的拉应力影响，由于生产过程中产生的残余应力，碟型弹簧的计算应力高于实际应力。基于不同的ho/t值，碟形弹簧横截面II点（下表面内边缘）或III（下表面外边缘）为最大拉应力点。

弹簧上表面内边缘，即横截面I点为最大压应力点，该应力直接影响弹簧的预压变形，该变形是由于变形量超出碟形弹簧材料的弹性极限而产生的塑性变形导致，从而使弹簧自由高度减

小。如下图

 

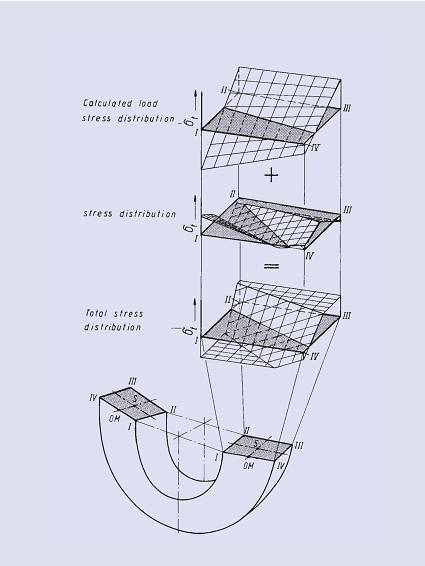
通过缩智短力臂加载的无支撑面碟形弹簧

对于曲线的变形模型来讲，载荷通过缩短的力臂加载，获得给定变形量时所需的力矩与通过横截面I点和III点加载时相同，而力臂的缩短则要求对弹簧施加更大的载荷，因此这种情况下获得的弹簧载荷特性曲线要比正常情况下陡峭。但弹簧计算载荷应力不受加载点影响，而只与弹簧锥角大小有关，如下图

 

有支撑面的碟形弹簧

支撑面仅用于厚度大于6mm的碟形弹簧（DIN2093标准，第三组）。采用支撑面使弹簧承载面积增大，从而减少导向件与弹簧之间的摩擦。承载点也由外边缘de变为de’，由内边缘di变为di’。这种变化导致力臂缩短、载荷特性曲线变陡。如下图

 

 

 

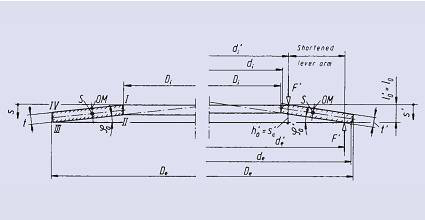
有支撑面碟形弹簧的设计载荷F（变形量S=0.75 •ho）与相同尺寸De、Di及lo的无支撑面碟型弹簧相同，这是由于支撑面的存在使力臂缩短而需要增加载荷，同时使厚度减薄而导致载荷减小，二者相互抵消。由于要求相同的自由高度lo，有支撑面的碟型弹簧须具有较大的锥角φo’>φo。这就导致其载荷特性曲线除立直高度点F’（s=0.75ho）F=(s=0.75ho)外，与标准碟形弹簧特性曲线略有偏差。

 

 

 

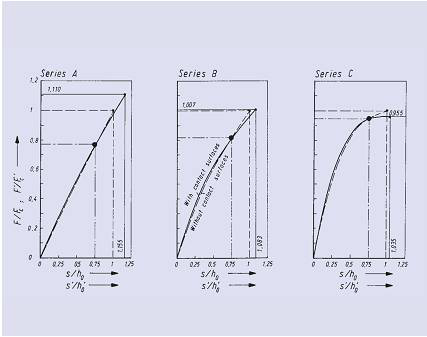
DIN2093标准详细规定了盘片厚度由t减到t’的情况。A、B系列弹簧t’与t之间的平均厚度减薄比为0.938，C系列弹簧t’与t之间的平均厚度比为0.995。由于支撑面的存在，已不必对横截面边缘I…IV角点的载荷应力进行计算。因此计算应力或多或少高于用更为精确的方法计算的角部实际应力。由于这些数值只是一些名义值，因此偏差并不重要。

特殊情况

特殊材料碟形弹簧

适用于矩形弹簧截面碟形弹簧特征方程计算出的弹簧承载力高于E=206000N/mm2、μ=0.3的弹簧钢达8%至9%，但可以通过由于I点和III点处的倒角引起的力臂缩短来补偿，因此该钢种碟型弹簧的计算载荷和实测载荷基本相近。但对于特殊材料，尤其是泊送比μ   较大的材料，这种情况不再成立。

极薄碟形弹簧

对于De/t＞40的极薄碟形弹簧，特性方程计算出的弹簧承载力过大，此时，碟形弹簧截面不再保持矩形，而且必须考虑到变形超出横截面的情况（特别是使用有限元分析）。

极小直径比碟形弹簧

计算De/Di＜1.8碟形弹簧的载荷特性曲线时，必须考虑由于倒角引起的力臂缩短，否则会出现计算承载力过低的现象。

 

 

                                               具体详见手册44-47